
11660번: 구간 합 구하기 5
첫째 줄에 표의 크기 N과 합을 구해야 하는 횟수 M이 주어진다. (1 ≤ N ≤ 1024, 1 ≤ M ≤ 100,000) 둘째 줄부터 N개의 줄에는 표에 채워져 있는 수가 1행부터 차례대로 주어진다. 다음 M개의 줄에는 네
www.acmicpc.net
⭐️ 코드
import java.io.BufferedReader;
import java.io.BufferedWriter;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.util.StringTokenizer;
// 구간 합 구하기 5
public class BJ_CT_3 {
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st = new StringTokenizer(br.readLine());
int N = Integer.parseInt(st.nextToken()); // 4
int M = Integer.parseInt(st.nextToken()); // 3
int[][] squared = new int[N + 1][N + 1]; // 좌표를 통해 사각형으로 만들어진 누적 합 배열
// 좌표를 통해 사각형으로 만들어진 누적 합 배열
// squared[i][j] = (1,1)에서 (i,j)까지의 합
for (int i = 1; i <= N; i++) {
st = new StringTokenizer(br.readLine());
for (int j = 1; j <= N; j++) {
// (왼쪽← 값) + (위에↑ 값) - (↖중복되는 대각선 값) + (input 값)
squared[i][j] = squared[i - 1][j] + squared[i][j - 1] - squared[i - 1][j - 1] + Integer.parseInt(st.nextToken());
}
}
for (int i = 0; i < M; i++) {
st = new StringTokenizer(br.readLine());
int x1 = Integer.parseInt(st.nextToken());
int y1 = Integer.parseInt(st.nextToken());
int x2 = Integer.parseInt(st.nextToken());
int y2 = Integer.parseInt(st.nextToken());
// 사각형에서 해당하지 않는 부분 차감 + 공통해서 빼는 부분 더하기
bw.write(squared[x2][y2] - squared[x2][y1 - 1] - squared[x1 - 1][y2] + squared[x1 - 1][y1 - 1] + "\n");
}
bw.flush();
}
}
💡 문제 풀이
구간 합 구하기 4 문제와 같은 누적 합(Prefix Sum) 알고리즘을 사용해서 푸는 문제다.
하지만 문제 4와 다르게 1차원 배열 형태가 아닌 2차원 배열 형태의 문제다.
조건을 먼저 살펴보자.
제한시간은 1초, O(N^2) 형태로 문제를 풀면
1 ≤ N ≤ 1024, 1 ≤ M ≤ 100,000 이므로
1,024,00,000번의 연산을 하게 되므로 시간 초과가 걸리기 때문에 O(N*logN) 이하의 형태로 풀어야 한다.
다음은 문제를 살펴보자.
문제를 잘 읽어보면 이 문제는 사각형을 그려서 그 안에서 값들의 합을 구하는 문제다.
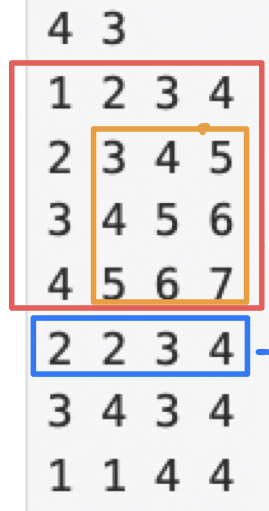
아래 사진을 참고해보자. (2,2), (3,4)의 위치에 존재하는 수들의 합을 구하는게 아니라 그 내부의 사각형(주황색 사각형)에 존재하는 수들을 다 더하는 것이다. 여기부터 이제 조금 어려워지기 시작한다.
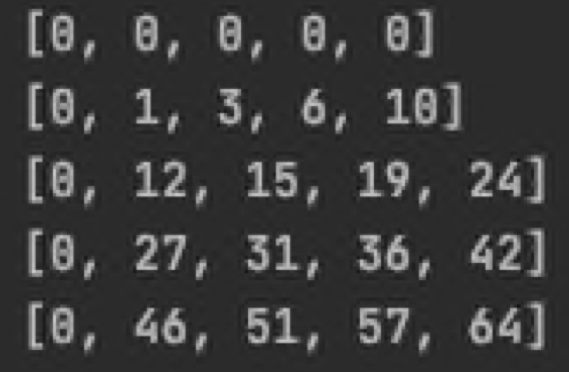
구간 합 구하기 4처럼 문제를 풀게 되면 아래와 같은 표를 만들게 될 것이다. 저렇게 하면 문제를 풀 수 없다.
이제 문제를 풀어보자.
우리는 표에서 (1,1) 부터 [ i, j ]까지의 합을 더한 수들의 누적 합을 만들 배열을 만들 것이다.
int[][] squared = new int[N + 1][N + 1]; // 좌표를 통해 사각형으로 만들어진 누적 합 배열그리고 그렇게 만들어진 표에 (1,1) 부터 [ i, j ]까지의 합을 집어넣는다.
// 좌표를 통해 사각형으로 만들어진 누적 합 배열
// squared[i][j] = (1,1)에서 (i,j)까지의 합
for (int i = 1; i <= N; i++) {
st = new StringTokenizer(br.readLine());
for (int j = 1; j <= N; j++) {
// (왼쪽← 값) + (위에↑ 값) - (↖중복되는 대각선 값) + (input 값)
squared[i][j] = squared[i - 1][j] + squared[i][j - 1] - squared[i - 1][j - 1] + Integer.parseInt(st.nextToken());
}
}처음부터 바로 input 값을 집어넣는 형태로 진행했다.
(1, 1) 부터 [ i, j ]까지의 합을 구하는 형태가 이해가 안될수도 있다. 아래 표를 참고해보자.

왼쪽 표는 일반적인 input 배열이고 오른쪽의 표는 누적 합을 더한 결과 배열이다. 이해가 더 쉬울 수 있게 아래 그림도 보자.
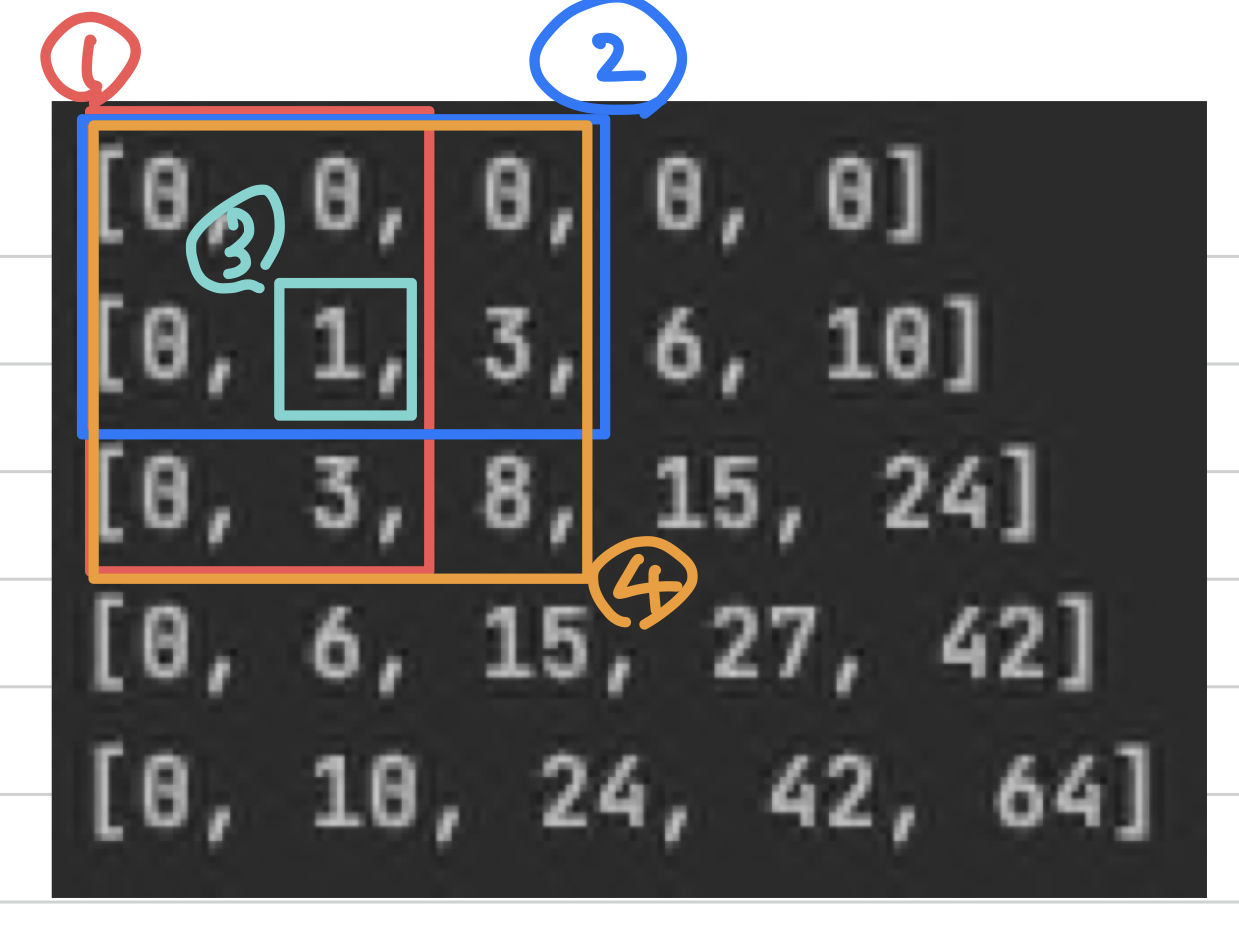
우리는 (2, 2)의 위치에 있는 값을 집어넣고 싶다고 할 때, 1번 박스와 2번 박스에서 누적된 값들의 합과, 3번 박스에서 알 수 있는 겹치는 값을 2번 더해주는 부분을 빼주고, 원래 (2, 2)의 위치의 값인 3을 더해주는 방식이다.
위 방식으로 쭉쭉 진행하다 보면 배열의 값은 사각형을 만드는 위치의 오른쪽 아래 꼭지점이 될 것이고 그게 (1, 1) 부터 [ i, j ]까지의 합이 되는 것이다.
자세한 풀이는 아래 포스팅을 참고하자..!
[백준] 11660번 - 구간 합 구하기 5
컴퓨터/IT/알고리즘 정리 블로그
chanhuiseok.github.io
우리는 결국 조건에 맞는 꼭지점에 위치한 사각형을 그렸을 때 그 내부의 값의 누적을 구해야 한다.
계산 식은 아래와 같고 방식은 위에서 설명한 것과 동일하다.
squared[x2][y2] - squared[x2][y1 - 1] - squared[x1 - 1][y2] + squared[x1 - 1][y1 - 1]👀 후기
누적 합 구하기 문제가 결국 비슷하다 해도 배열의 차원의 개수가 달라지면 풀이도 달라지게 된다. 그렇게 되면 이해하기가 힘들고 접근 방식도 어려워진다... 수학적인 지식을 정말 많이 요구하기 때문에 힘겹게 풀었다....
어렵다....
'CodingTest > BOJ' 카테고리의 다른 글
| [백준 / 11650번] 좌표 정렬하기 - (Java - TimSort - 정렬) (0) | 2023.02.08 |
|---|---|
| [백준 / 10989번] 수 정렬하기 3 - (Java - Counting Sort / 개수 정렬) (0) | 2023.02.08 |
| [백준 / 17298번] 오큰수 - (Java - Stack) (0) | 2023.01.21 |
| [백준 / 11659번] 구간 합 구하기4 - (Java - 누적 합) (2) | 2023.01.08 |
| [백준 / 1002번] 터렛 - (Java - 수학) (0) | 2022.12.22 |