
11659번: 구간 합 구하기 4
첫째 줄에 수의 개수 N과 합을 구해야 하는 횟수 M이 주어진다. 둘째 줄에는 N개의 수가 주어진다. 수는 1,000보다 작거나 같은 자연수이다. 셋째 줄부터 M개의 줄에는 합을 구해야 하는 구간 i와 j
www.acmicpc.net

⭐️ 코드
import java.io.*;
import java.util.StringTokenizer;
public class 구간_합_구하기4 {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st = new StringTokenizer(br.readLine()); // 5 3
int N = Integer.parseInt(st.nextToken()); // 5
int M = Integer.parseInt(st.nextToken()); // 3
int[] input = new int[N + 1]; // 누적해서 더한 값을 담을 배열
st = new StringTokenizer(br.readLine()); // 5 4 3 2 1
// 배열의 index[0]은 제외하고 [1]부터 시작
input[1] = Integer.parseInt(st.nextToken());
for (int i = 2; i <= N; i++) {
// 누적합 알고리즘 사용
// input 배열에 index별로 앞에서 부터 값을 더해서 누적된 값 입력
input[i] = input[i-1] + Integer.parseInt(st.nextToken());
}
for(int i = 1; i<=M; i++) {
// 1 3, 2 4, 5 5
st = new StringTokenizer(br.readLine());
int a = Integer.parseInt(st.nextToken());
int b = Integer.parseInt(st.nextToken());
bw.write((input[b]-input[a-1]) + "\n");
}
bw.flush();
}
}
💡 문제 풀이
문제를 처음 풀게 되면 간단하게 포문을 통해 i번째 수부터 j번째 수까지 합을 구할 수 있긴 하다.
하지만 그렇게 풀게 되면 시간복잡도 측면에서 오류가 생기게 된다.
우리는 최악의 경우를 생각해야 한다. 최악의 경우에는 조건에서 N은 100,000개의 숫자가 주어지고 합을 구해야 하는 i와 j는 1부터 100,000개가 되기 때문에 총연산은 100,000 * 100,000번의 연산을 거쳐야 한다. -> 10,000,000,000(100억 번)
기본적으로 컴퓨터 CPU는 1초에 1억 번의 연산을 한다고 한다. 그렇지만 100억 번의 연산이라면 100초의 시간이 걸리게 되는 것이다.
일반적인 이중 for문을 통해 풀게 되면 시간복잡도는 O(N^2)의 시간이 걸리게 되고, O(N^2) 형태로 문제를 풀면 정말 100억 번의 연산을 처리해야 한다.
우리가 푸는 문제의 시간제한은 1초 이기 때문에 무조건적으로 시간제한이 걸리게 된다. 성능을 끌어올려야 한다.
Big-O 표기법

구간 합 구하기 4 문제에서 주어지는 시간 복잡도는 O(N^2)이 아닌 O(N*logN) 이하의 방식을 써야지 풀 수 있다.
수학에서는 log에서 아래 10을 생략하지만 컴퓨터에서는 2를 생략하게 된다.
컴퓨터에서 10만*log(10만) 은 10만 * 2^16 정도이다.
따라서 O(N*logN)을 이용하면 100억의 연산은 약 160만 회의 연산으로 줄어들게 된다.
10,000,000,000 -> 1,600,000
이 문제에서는 누적 합(Prefix Sum)이라는 알고리즘을 사용하면 O(N) 정도의 시간으로 풀 수 있다.
간단하게 설명하자면 i부터 j까지의 숫자를 input [ ]이라는 배열에 각 인덱스에 [i-1] + [i], [i-1] + [i+1], [i-1] + [i+2]... [i-1] + [i+j] 형식으로 누적해서 값을 넣어주는 형태다.
문제를 풀어보며 누적 합 알고리즘에 대해 알아보자.
int[] input = new int[N + 1]; // 누적해서 더한 값을 담을 배열
우리는 i~j까지의 합을 구해야 하는데 주어지는 i 값은 1부터 주어지기 때문에 배열의 0번째는 비워두고 1번부터 채워나갈 생각이다.
// 배열의 index[0]은 제외하고 [1]부터 시작
input[1] = Integer.parseInt(st.nextToken());
for (int i = 2; i <= N; i++) {
// 누적합 알고리즘 사용
// input 배열에 index별로 앞에서 부터 값을 더해서 누적된 값 입력
input[i] = input[i-1] + Integer.parseInt(st.nextToken());
}input 배열에는 입력받은 숫자를 그대로 입력하는 것이 아닌 누적된 합에 대한 값을 입력하게 된다.
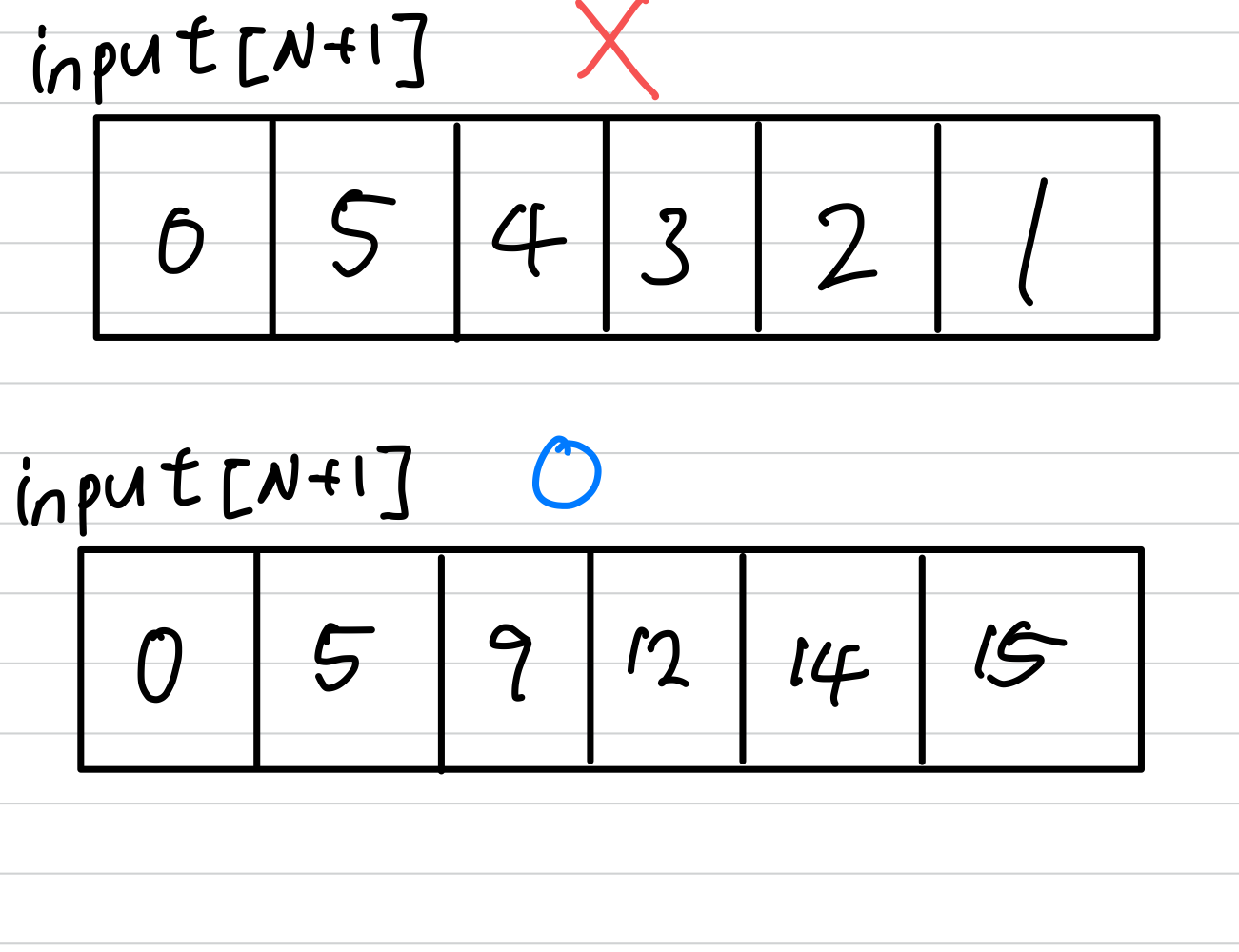
이렇게 입력하게 되면 우리는 for문을 계속 돌리며 값을 하나씩 더해가는 것이 아닌 j번째에서 [i-1] 값을 빼주기만 하면 i부터 j까지의 합을 바로 구할 수 있다.
for(int i = 1; i<=M; i++) {
// 1 3, 2 4, 5 5
st = new StringTokenizer(br.readLine());
int a = Integer.parseInt(st.nextToken());
int b = Integer.parseInt(st.nextToken());
bw.write((input[b]-input[a-1]) + "\n");
}
연산 횟수가 획기적으로 줄어들기 때문에 누적 합(Prefix Sum) 알고리즘 꼭 기억해 두자.
👀 후기
코테 강의를 들으며 빅오표기법 관련해서 시간복잡도를 계산하는 방법을 알았다.
조건을 꼭 보고 그 조건에서 최악의 결과를 미리 생각해서 어떤 변수형을 쓸지, 어떻게 시간초과가 나지 않도록 구상할지 미리 설계하고 코딩테스트를 풀라는 말이 정말 크게 와닿았다.
앞으로 제한사항과 조건을 보고 코딩을 할 예정이다.
'CodingTest > BOJ' 카테고리의 다른 글
| [백준 / 11650번] 좌표 정렬하기 - (Java - TimSort - 정렬) (0) | 2023.02.08 |
|---|---|
| [백준 / 10989번] 수 정렬하기 3 - (Java - Counting Sort / 개수 정렬) (0) | 2023.02.08 |
| [백준 / 17298번] 오큰수 - (Java - Stack) (0) | 2023.01.21 |
| [백준 / 11660번] 구간 합 구하기5 - (Java - 누적 합) (0) | 2023.01.09 |
| [백준 / 1002번] 터렛 - (Java - 수학) (0) | 2022.12.22 |